k Shortest Paths in AQL
General query ideaPermalink
This type of query finds the first k paths in order of length (or weight) between two given documents, startVertex and targetVertex in your graph.
Every such path will be returned as a JSON object with three components:
- an array containing the
verticeson the path - an array containing the
edgeson the path - the
weightof the path, that is the sum of all edge weights
If no weightAttribute is given, the weight of the path is just its length.
Example
Let us take a look at a simple example to explain how it works. This is the graph that we are going to find some shortest path on:
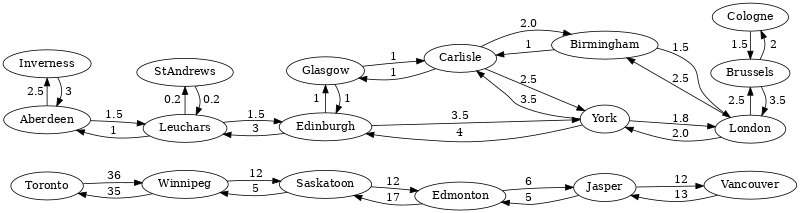
Each ellipse stands for a train station with the name of the city written inside of it. They are the vertices of the graph. Arrows represent train connections between cities and are the edges of the graph. The numbers near the arrows describe how long it takes to get from one station to another. They are used as edge weights.
Let us assume that we want to go from Aberdeen to London by train.
We expect to see the following vertices on the shortest path, in this order:
- Aberdeen
- Leuchars
- Edinburgh
- York
- London
By the way, the weight of the path is: 1.5 + 1.5 + 3.5 + 1.8 = 8.3.
Let us look at alternative paths next, for example because we know that the direct connection between York and London does not operate currently. An alternative path, which is slightly longer, goes like this:
- Aberdeen
- Leuchars
- Edinburgh
- York
- Carlisle
- Birmingham
- London
Its weight is: 1.5 + 1.5 + 3.5 + 2.0 + 1.5 = 10.0.
Another route goes via Glasgow. There are seven stations on the path as well, however, it is quicker if we compare the edge weights:
- Aberdeen
- Leuchars
- Edinburgh
- Glasgow
- Carlisle
- Birmingham
- London
The path weight is lower: 1.5 + 1.5 + 1.0 + 1.0 + 2.0 + 1.5 = 8.5.
SyntaxPermalink
The syntax for k Shortest Paths queries is similar to the one for
Shortest Path and there are also two options to
either use a named graph or a set of edge collections. It only emits a path
variable however, whereas SHORTEST_PATH emits a vertex and an edge variable.
It is highly recommended that you use a LIMIT statement, as k Shortest Paths is a potentially expensive operation. On large connected graphs it can return a large number of paths, or perform an expensive (but unsuccessful) search for more short paths.
Working with named graphsPermalink
FOR path
IN OUTBOUND|INBOUND|ANY K_SHORTEST_PATHS
startVertex TO targetVertex
GRAPH graphName
[OPTIONS options]
[LIMIT offset, count]
FOR: emits the variable path which contains one path as an object containingvertices,edges, and theweightof the path.INOUTBOUND|INBOUND|ANY: defines in which direction edges are followed (outgoing, incoming, or both)K_SHORTEST_PATHS: the keyword to compute k Shortest Paths- startVertex
TOtargetVertex (both string|object): the two vertices between which the paths will be computed. This can be specified in the form of a ID string or in the form of a document with the attribute_id. All other values will lead to a warning and an empty result. If one of the specified documents does not exist, the result is empty as well and there is no warning. GRAPHgraphName (string): the name identifying the named graph. Its vertex and edge collections will be looked up.OPTIONSoptions (object, optional): used to modify the execution of the traversal. Only the following attributes have an effect, all others are ignored:- weightAttribute (string): a top-level edge attribute that should be used to read the edge weight. If the attribute does not exist or is not numeric, the defaultWeight will be used instead. The attribute value must not be negative.
- defaultWeight (number): this value will be used as fallback if there is
no weightAttribute in the edge document, or if it’s not a number. The value
must not be negative. The default is
1.
LIMIT(see LIMIT operation, optional): the maximal number of paths to return. It is highly recommended to use aLIMITforK_SHORTEST_PATHS.
k Shortest Paths traversals do not support negative weights. If a document
attribute (as specified by weightAttribute) with a negative value is
encountered during traversal, or if defaultWeight is set to a negative
number, then the query is aborted with an error.
Working with collection setsPermalink
FOR path
IN OUTBOUND|INBOUND|ANY K_SHORTEST_PATHS
startVertex TO targetVertex
edgeCollection1, ..., edgeCollectionN
[OPTIONS options]
[LIMIT offset, count]
Instead of GRAPH graphName you can specify a list of edge collections.
The involved vertex collections are determined by the edges of the given
edge collections.
Traversing in mixed directionsPermalink
For k shortest paths with a list of edge collections you can optionally specify the
direction for some of the edge collections. Say for example you have three edge
collections edges1, edges2 and edges3, where in edges2 the direction
has no relevance, but in edges1 and edges3 the direction should be taken into
account. In this case you can use OUTBOUND as general search direction and ANY
specifically for edges2 as follows:
FOR vertex IN OUTBOUND K_SHORTEST_PATHS
startVertex TO targetVertex
edges1, ANY edges2, edges3
All collections in the list that do not specify their own direction will use the
direction defined after IN (here: OUTBOUND). This allows to use a different
direction for each collection in your path search.
ExamplesPermalink
We load an example graph to get a named graph that reflects some possible train connections in Europe and North America.

Suppose we want to query a route from Aberdeen to London, and
compare the outputs of SHORTEST_PATH and K_SHORTEST_PATHS with
LIMIT 1. Note that while SHORTEST_PATH and K_SHORTEST_PATH with
LIMIT 1 should return a path of the same length (or weight), they do
not need to return the same path.
Using SHORTEST_PATH:
Using K_SHORTEST_PATHS:
With K_SHORTEST_PATHS we can ask for more than one option for a route:
If we ask for routes that don’t exist we get an empty result (from Aberdeen to Toronto):
FOR p IN OUTBOUND K_SHORTEST_PATHS 'places/Aberdeen' TO 'places/Toronto'
GRAPH 'kShortestPathsGraph'
LIMIT 3
RETURN {
places: p.vertices[*].label,
travelTimes: p.edges[*].travelTime,
travelTimeTotal: SUM(p.edges[*].travelTime)
}
[]
We can use the attribute travelTime that connections have as edge weights to take into account which connections are quicker. A high default weight is set, to be used if an edge has no travelTime attribute (not the case with the example graph). This returns the top three routes with the fewest changes and favoring the least travel time for the connection Saint Andrews to Cologne:
And finally clean up by removing the named graph:
arangosh> var examples = require("@arangodb/graph-examples/example-graph.js");
arangosh> examples.dropGraph("kShortestPathsGraph");

